Unsere neue Lösungsstrategie für den MedAT-Untertest „Figuren zusammensetzen“
Im MedAT-Untertest „Figuren zusammensetzen“ ist es seit diesem Jahr nicht mehr erlaubt, Linien, Punkte oder andere Hilfsmittel zur Lösung zu verwenden. Das bedeutet für die meisten eine große Umstellung ihrer Lösungsstrategie.
Wir haben auf diese Änderungen reagiert und eine neue Strategie entwickelt, die sich auf viele der Aufgaben anwenden lässt. Diese haben wir euch in einem kostenlosen öffentlichen Webinar präsentiert. Für alle, die das Webinar verpasst haben, gibt es hier eine Zusammenfassung und Erläuterung unserer neuen „MedBooster-Strategie“.
Der Untertest „Figuren zusammensetzen“
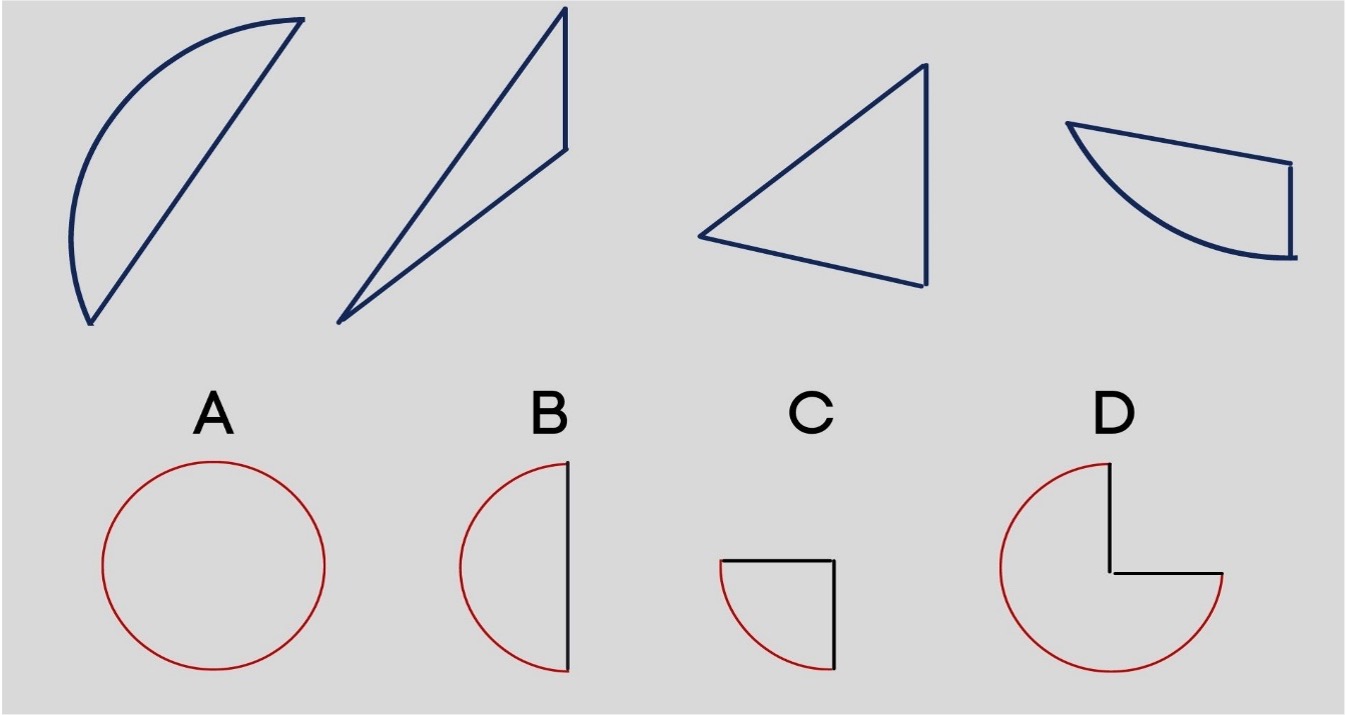
In diesem Untertest sind vier bis fünf Teile einer geometrischen Figur abgebildet. Durch das Zusammensetzen der Einzelteile muss herausgefunden werden, welche Figur zerschnitten wurde. Dabei kann eine der angegebenen Figuren (Antwortmöglichkeiten A-D) oder keine davon richtig sein (Antwortmöglichkeit E).
Tricky! Denn die Einzelteile müssen ausschließlich im Kopf, ohne jeglichen Gebrauch von Hilfsmitteln, zusammengesetzt werden. Außerdem sind die Einzelteile meist nicht mehr in ihrer ursprünglichen Größe, sondern vergrößert abgebildet. Das macht es noch schwerer…
Doch keine Panik, denn mit dieser Methode, die sich auf alle kreisförmigen Figuren anwenden lässt, habt ihr die Hälfte der Punkte schon eingesackt.
Die Strategie
Wir werden euch die Methode anhand eines Beispiels erklären. Oben aufgeführt seht ihr die Einzelstücke, welche zusammengeführt einen der unteren Viertel-, Halb-, Dreiviertel- oder vollen Kreis ergeben können (im Untertest sind diese ausgefüllt, hier nur zur Vereinfachung Linien ohne Füllfarbe).
Wenn man nun die Fläche aller oberen Stücke mit der Fläche von jeweils einer der kreisförmigen Figuren vergleicht, so fällt auf, dass die Fläche der oberen Teile viel größer ist, als die der Kreise. Das ist die oben bereits erwähnte Vergrößerung der Einzelstücke. Eine Lösung der Aufgabe durch einen Flächenvergleich ist also nicht möglich. Was nun?
Wir betrachten zunächst die unteren Kreise, die vier Antwortmöglichkeiten. Den Fokus setzen wir jetzt ausschließlich auf den roten, gekrümmten Teil des Kreises. Die schwarzen Stücke sind für die Lösungsstrategie irrelevant. Nun betrachten wir die Länge der jeweiligen gekrümmten Stücke der Kreise. Antwort A ist ein voller Kreis, er hat von allen das längste gekrümmte Stück. Antwort B ist ein Halbkreis, der hat natürlich nur ein halb so langes, gekrümmtes Stück wie das von Antwort A. Antwort C ist ein Viertelkreis und hat somit das allerkürzeste gekrümmte Stück von allen. Und Antwort D hat ein fast so langes gekrümmtes Stück wie Antwort A. Aber natürlich nicht ganz so lang, klar.
So, jetzt kommt Schritt zwei. Das kann man sich tatsächlich sehr gut mit drei gekochten Spaghetti vorstellen (klingt blöd, ist es aber gar nicht mal so 😊 ). Ihr sollt nun mit diesen drei biegsamen Nudeln jeweils den gekrümmten Teil des Kreises auslegen, also die Spaghetti auf die Kreislinien legen. Fangen wir mit Antwort A, dem vollen Kreis an. In eurem Kopf habt ihr nun diesen mit drei Spaghetti umrandeten Kreis. Dasselbe Spiel mit Antwort B, mit den drei gleichen Spaghetti. Wichtig: Die Fläche des Kreises spielt überhaupt keine Rolle. Das haben wir oben ja festgestellt, dass das kein verlässliches Kriterium ist. Der Fokus liegt absolut nur auf den Krümmungen!
Jetzt vergleichen wir beide „Spaghetti-Krümmungen“. Beim vollen Kreis sind die Spaghetti recht stark gekrümmt, die Spaghetti mussten enger gelegt werden, weil der Umfang des Kreises ja größer ist. Beim halben sind sie viel weniger gekrümmt. Wenn ihr euch das schwer vorstellen könnt, probiert es wirklich mal aus, dann wird’s „Klick“ machen.
Zusammengefasst: Je kürzer das gekrümmte Stück, desto weniger müssen die Teile, die diesen Kreis zusammengesetzt abbilden, gebogen sein.
Denn genau dieses Verhältnis zwischen Länge der Krümmung und die Krümmung seines herausgeschnittenen Stückes machen wir uns in diesem Untertest zu Nutze.
Jetzt gehen wir die Beispielaufgabe exemplarisch mal durch. Schauen wir uns das hintere Teil an. Man sieht, dass es gekrümmt ist, jedoch nicht sonderlich stark. Ein ganzer Kreis, also Antwort A, kann somit ausgeschlossen werden. Für einen Drittelkreis ist es ebenfalls zu schwach gekrümmt, Antwort D fliegt raus. Bleiben uns B und C als Möglichkeiten. Jetzt betrachten wir das erste der vier Teile. Hier ist das gekrümmte Stück recht lang, für einen Viertelkreis ist es im Vergleich zur Länge zu schwach gebogen. Somit kommt Antwort B, der Halbkreis, in Betracht. Zwar gibt es im MedAT immer noch Antwortmöglichkeit E, dass die Teile keine dieser Figuren zugeordnet werden können, doch zieht man nun alle Einzelteile zusammen in Betracht, so ergibt sich, das Antwort B sehr wahrscheinlich ist.
Konklusion: Im MedAT sind circa die Hälfte der Figuren in diesem Untertest Kreisformen. Der Fokus sollte auf der Krümmung der Kreise liegen. Stück für Stück können die Krümmungen verglichen und eine Antwort nach der anderen ausgeschlossen werden.
Übung macht den Meister! Schult euer Auge in Bezug auf die Krümmungen. Lernt, wie stark die Krümmung eines vollen, Halb-, Dreiviertel- und Viertelkreises ausschaut, unabhängig von der Kreisgröße.
Autorin: Sophie Meisen, Medizinstudentin und MedBooster-Bloggerin

